WooCommerce 8: A Six-Month Retrospective
WooCommerce is one of the most popular eCommerce plugins for WordPress and with good reason. Its…

WooCommerce is one of the most popular eCommerce plugins for WordPress and with good reason. Its…

WordPress plugins add functionality and features to your website, helping you customize it to your specific…

Download Opera for free using https://opr.as/Opera-browser-anastasiintech Thanks Opera for sponsoring this video! Timestamps:00:00 – Intro00:52 –…

Jerome Pesenti has a few reasons to celebrate Meta’s decision last week to release Llama 3,…

Have you heard the slogan “For the community, by the community”? You may have many times,…

Jason Matheny is a delight to speak with, provided you’re up for a lengthy conversation about…

In today’s bustling world, distractions are as ubiquitous as air. To not get swept away by…

When it comes to diets there is so much conflicting information out there, it’s no wonder…

We all know how important website security is, right? We hope you said “yes” because it…

Two of the biggest deepfake pornography websites have now started blocking people trying to access them…

Every picture and video you post spills secrets about you, maybe even revealing where you live….

I was recently waiting for my nails to dry and didn’t want to smudge the paint,…

In the bustling heart of tech, where new ideas sprout faster than we can tend to…

In the bustling landscape of today’s work environment, where demands are like tectonic plates — constantly…

Get your Laifen Wave electronic toothbrush now! ⬇️⮕ Official website: https://bit.ly/48JBKsr⮕ Amazon ABS White: https://amzn.to/3V4OHtq⮕ Amazon…

Last October, I received an email with a hell of an opening line: “I fired a…
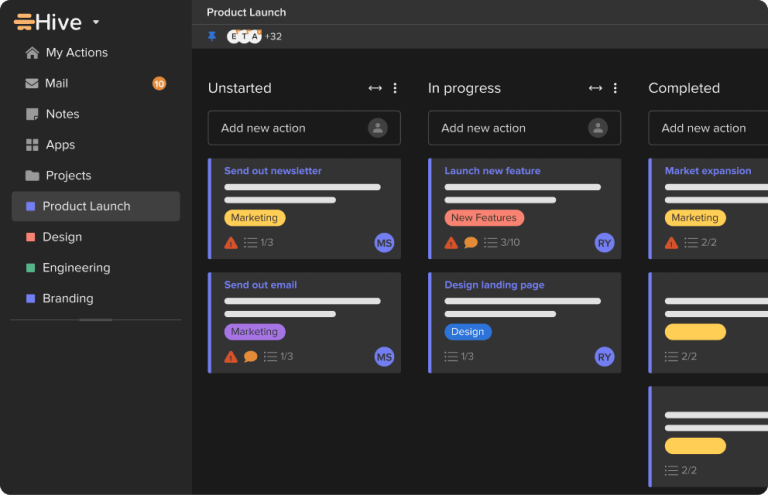
Did you know that a staggering 1 in 8 people never feel under control at work?…