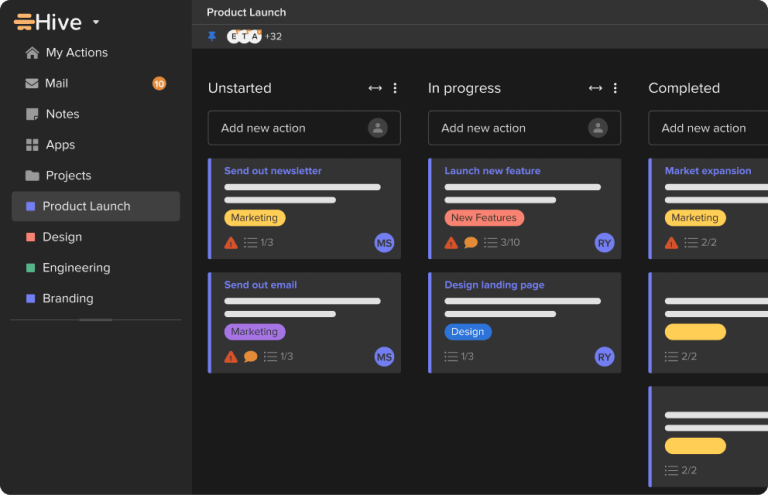
WooCommerce 8: A Six-Month Retrospective

WooCommerce is one of the most popular eCommerce plugins for WordPress and with good reason. Its responsive design, SEO-friendliness, and many efficient and excellent features make it an eCommerce platform that many users trust. Over 40% of WordPress users who…