An Introduction to Genetic Algorithms

A genetic algorithm is a procedure that searches for the best solution to a problem using operations that emulate the natural processes involved in evolution, such as “survival of the fittest”, chromosomal crossover, and mutation. This article provides a gentle introduction to writing genetic algorithms, discusses some important considerations when writing your own algorithm, and presents a few examples of genetic algorithms in action.

Guessing the Unknown

The year is 2369 and humankind has spread out across the stars. You’re a young, bright doctor stationed at a star base in deep space that’s bustling with interstellar travelers, traders, and the occasional ne’er-do-well. Almost immediately after your arrival, one of the station’s shopkeeps takes an interest in you. He claims to be nothing more than a simple tailor, but rumors say he’s black ops working for a particularly nasty regime.

The two of you begin to enjoy weekly lunches together and discuss everything from politics to poetry. Even after several months, you still aren’t certain whether he’s making romantic gestures or fishing for secrets (not that you know any). Perhaps it’s a bit of both.

One day over lunch he presents you with this challenge: “I have a message for you, dear doctor! I can’t say what it is, of course. But I will tell you it’s 12 characters long. Those characters can be any letter of the alphabet, a space, or punctuation mark. And I’ll tell you how far off your guesses are. You’re smart; do you think you can figure it out?”

You return to your office in the medical bay still thinking about what he said. Suddenly, a gene sequencing simulation you left running on a nearby computer as part of an experiment gives you an idea. You’re not a code breaker, but maybe you can leverage your expertise in genetics to figure out his message!

A Bit of Theory

As I mentioned at the beginning, a genetic algorithm is a procedure that searches for a solution using operations that emulate processes that drive evolution. Over many iterations, the algorithm selects the best candidates (guesses) from a set of possible solutions, recombines them, and checks which combinations moved it closer to a solution. Less beneficial candidates are discarded.

In the scenario above, any character in the secret message can be A–Z, a space, or a basic punctuation mark. Let’s say that gives us the following 32-character “alphabet” to work with: ABCDEFGHIJKLMNOPQRSTUVWXYZ -.,!? This means there are 32¹² (roughly 1.15Ã—10¹⁸) possible messages, but only one of those possibilities is the correct one. It would take too long to check each possibility. Instead, a genetic algorithm will randomly select 12 characters and ask the tailor/spy to score how close the result is to his message. This is more efficient than a brute-force search, in that the score lets us fine-tune future candidates. The feedback gives us the ability to gauge the fitness of each guess and hopefully avoid wasting time on the dead-ends.

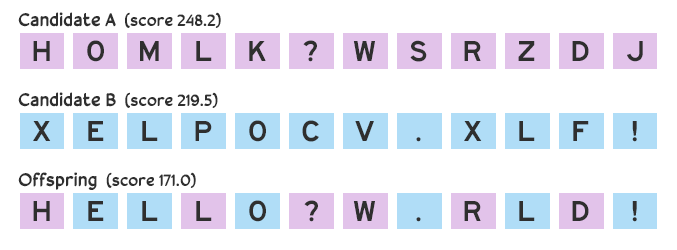
Suppose we make three guesses: HOMLK?WSRZDJ, BGK KA!QTPXC, and XELPOCV.XLF!. The first candidate receives a score of 248.2, the second receives 632.5, and the third receives 219.5. How the score is calculated depends on the situation, which we’ll discuss later, but for now let’s assume it’s based on deviation between the candidate and target message: a perfect score is 0 (that is, there are no deviations; the candidate and the target are the same), and a larger score means there’s a greater deviation. The guesses that scored 248.2 and 219.5 are closer to what the secret message might be than the guess that scored 635.5.

Future guesses are made by combining the best attempts. There are many ways to combine candidates, but for now we’ll consider a simple crossover method: each character in the new guess has a 50–50 chance of being copied from the first or second parent candidate. If we take the two guesses HOMLK?WSRZDJ and XELPOCV.XLF!, the first character of our offspring candidate has a 50% chance of being H and 50% chance of being X, the second character will be either O or E, and so on. The offspring could be HELLO?W.RLD!.

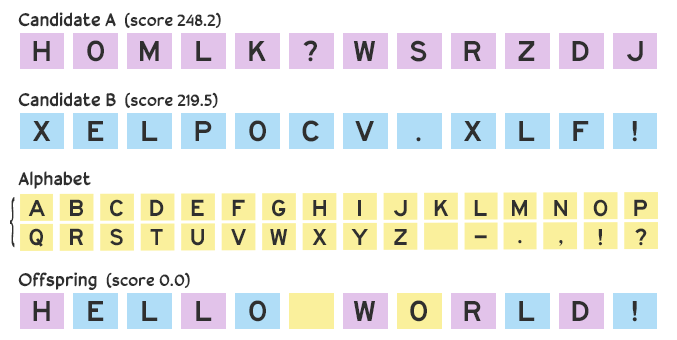
However, a problem can arise over multiple iterations if we only use values from the parent candidates: a lack of diversity. If we have one candidate consisting of all A’s and another of all B’s, then any offspring generated with them solely by crossover would consist only of A’s and B’s. We’re out of luck if the solution contains a C.

To mitigate this risk and maintain diversity while still narrowing in on a solution, we can introduce minor changes. Rather than a straight 50–50 split, we afford a small chance that an arbitrary value from the alphabet is picked instead. With this mutation the offspring might become HELLO WORLD!.

Unsurprisingly, genetic algorithms borrow a lot of vocabulary from genetic science. So before we go much further, let’s refine some of our terminology:

Allele: a member of the genetic alphabet. How alleles are defined depends on the algorithm. For example, 0 and 1 might be alleles for a genetic algorithm working with binary data, an algorithm working with code might use function pointers, etc. In our secret message scenario, the alleles were the letters of the alphabet, space, and various punctuation.
Chromosome: a given sequence of alleles; a candidate solution; a “guess”. In our scenario, HOMLK?WSRZDJ, XELPOCV.XLF!, and HELLO WORLD! are all chromosomes.
Gene: the allele at a specific location in the chromosome. For the chromosome HOMLK?WSRZDJ, the first gene is H, the second gene is O, the third is M, and so on.
Population: a collection of one or more candidate chromosomes proposed as a solution to the problem.
Generation: the population during a specific iteration of the algorithm. The candidates in one generation provide genes to produce the next generation’s population.
Fitness: a measure that evaluates a candidate’s closeness to the desired solution. Fitter chromosomes are more likely to pass their genes to future candidates while less fit chromosomes are more likely to be discarded.
Selection: the process of choosing some candidates to reproduce (used to create new candidate chromosomes) and discarding others. Multiple selection strategies exist, which vary in their tolerance for selecting weaker candidates.
Reproduction: the process of combining genes from one or more candidates to produce new candidates. The donor chromosomes are called parents, and the resulting chromosomes are called as offspring.
Mutation: the random introduction of aberrant genes in offspring to prevent the loss of genetic diversity over many generations.