Pure CSS Bezier Curve Motion Paths

Are you a Bezier curve lover like I am?

Besides being elegant, Bezier curves have nice mathematical properties due to their definition and construction. No wonder they are widely used in so many areas:

• As a drawing/design tool: They are often refered to as “paths” in vector drawing software.
• As a format of representing curves: They are used in SVG, fonts and many other vector graphic formats.
• As a mathematical function: Often used to control animation timing.

Now, how about using Bezier curves as motion paths with CSS?

Quick Recap

Depending on the context, when referring to a “Bezier curve”, we often assume a 2D cubic Bezier curve.

Such a curve is defined by four points:

Note: In this article, we generally refer to P0 and P3 as endpoints, P1 and P2 as control points.

The word “cubic” means the underlying function of the curve is a cubic polynomial. There are also “quadratic” Bezier curves, which are similar, but with one fewer control point.

The Problem

Say you are given an arbitrary 2D cubic Beizer curve, how would you animate an element with pure CSS animation, such that it moves precisely along the curve?

As an example, how would you recreate this animation?

In this article we will explore three methods with different flavors. For each solution we will present an interactive demo, then explain how it works. There are lots of mathematical calculations and proofs behind the scene, but don’t worry, we will not go very deep.

Let’s start!

Method 1: Time Warp

Here’s the basic idea:

• Set up @keyframes to move the element from one endpoint of the curve to the other.
• Distort the time for each coordinate individually, using animation-timing-function.

Note: There are lots of examples and explanations in Temani Afif’s article (2021).

Using the cubic-bezier() function with correct parameters, we can create a motion path of any cubic Bezier curve:

This demo shows a pure CSS animation. Yet canvas and JavaScript are used, which serve two purposes:

• Visualize the underlying Bezier curve (red curve).
• Allow adjusting the curve with the typical “path” UI.

You can drag the two endpoints (black dots) and the two control points (black squares). The JavaScript code will update the animation accordingly, by updating a few CSS variables.

Note: Here’s a pure CSS version for reference.

How it works

Suppose the desired cubic Bezier curve is defined by four points: p0, p1, p2, and p3. We set up CSS rules as following:

/* pseudo CSS code */
div { animation-name: move-x, move-y; /* Define: f(x, a, b) = (x - a) / (b - a) qx1 = f(p1.x, p0.x, p3.x) qx2 = f(p2.x, p0.x, p3.x) qy1 = f(p1.y, p0.y, p3.y) qy2 = f(p2.y, p0.y, p3.y) */ animation-timing-function: cubic-bezier(1/3, qx1, 2/3, qx1), cubic-bezier(1/3, qy1, 2/3, qy2);
} @keyframes move-x { from { left: p0.x; } to { left: p3.x; }
} @keyframes move-y { from { top: p0.y; } to { top: p3.y; }
}

The @keyframes rules move-x and move-y determine the starting and finishing locations of the element. In animation-timing-function we have two magical cubic-bezier() functions, the parameters are calculated such that both top and left always have the correct values at any time.

I’ll skip the math, but I drafted a brief proof here, for your curious math minds.

Discussions

This method should work well for most cases. You can even make a 3D cubic Bezier curve, by introducing another animation for the z value.

However there are a few minor caveats:

• It does not work when both endpoints lie on a horizontal or vertical line, because of the division-by-zero error.

Note: In practice, you can just add a tiny offset as a workaround.

• It does not support Bezier curves with an order higher than 3.
• Options for animation timing are limited.
  • We use 1/3 and 2/3 above to achieve a linear timing.
  • You can tweak both values to adjust the timing, but it is limited compared with other methods. More on this later.

Method 2: Competing Animations

As a warm-up, imagine an element with two animations:

div { animation-name: move1, move2;
}

What is the motion path of the element, if the animations are defined as following:

@keyframes move1 { to { left: 256px; }
} @keyframes move2 { to { top: 256px; }
}

As you may have guessed, it moves diagonally:

Now, what if the animations are defined like this instead:

@keyframes move1 { to { transform: translateX(256px); }
} @keyframes move2 { to { transform: translateY(256px); }
}

“Aha, you cannot trick me!” you might say, as you noticed that both animations are changing the same property, “move2 must override move1 like this:”

Well, earlier I had thought so, too. But actually we get this:

The trick is that move2 does not have a from frame, which means the starting position is animated by move1.

In the following demo, the starting position of move2 is visualized as the moving blue dot:

Quadratic Bezier Curves

The demo right above resembles the construction of a quadratic Bezier curve:

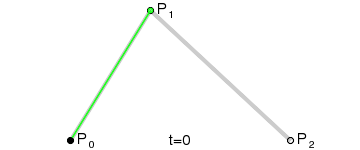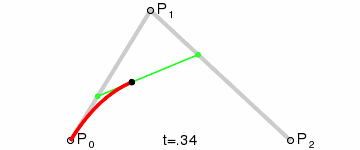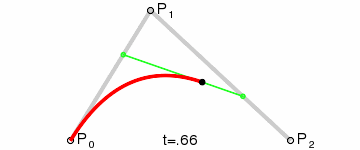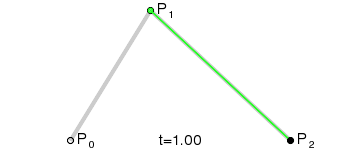
But they look different. The construction has three linearly moving dots (two green, one black), but our demo has only two (the blue dot and the target element).

Actually the motion path in the demo is a quadratic Bezier curve, we just need to tune the keyframes carefully. I will skip the math and just reveal the magic:

Suppose a quadratic Bezier curve is defined by points p0, p1, and p2. In order to move an element along the curve, we do the following:

/* pseudo-CSS code */
div { animation-name: move1, move2;
} @keyframes move1 { from { transform: translate3d(p0.x, p0.y, p0.z); } /* define q1 = (2 * p1 - p2) */ to { transform: translate3d(q1.x, q1.y, q1.z); }
} @keyframes move2 { to { transform: translate3d(p2.x, p2.y, p2.z); }
}

Similar to the demo of Method 1, you can view or adjust the curve. Additionally, the demo also shows two more pieces of information:

• The mathematical construction (gray moving parts)
• The CSS animations (blue parts)

Both can be toggled using the checkboxes.

Cubic Bezier Curves

This method works for cubic Bezier curves as well. If the curve is defined by points p0, p1, p2, and p3. The animations should be defined like this:

/* pseudo-CSS code */
div { animation-name: move1, move2, move3;
} @keyframes move1 { from { transform: translate3d(p0.x, p0.y, p0.z); } /* define q1 = (3 * p1 - 3 * p2 + p3) */ to { transform: translate3d(q1.x, q1.y, q1.z); }
} @keyframes move2 { /* define q2 = (3 * p2 - 2 * p3) */ to { transform: translate3d(q2.x, q2.y, q2.z); }
} @keyframes move3 { to { transform: translate3d(p3.x, p3.y, p3.z); }
}

Extensions

What about 3D Bezier Curves? Actually, the truth is, all the previous examples were 3D curves, we just never bothered with the z values.

What about higher-order Bezier curves? I am 90% sure that the method can be naturally extended to higher orders. Please let me know if you have worked out the formula for fourth-order Bezier curves, or even better, a generic formula for Bezier curves of order N.

Method 3: Standard Bezier Curve Construction

The mathematical construction of Bezier Curves already gives us a good hint.

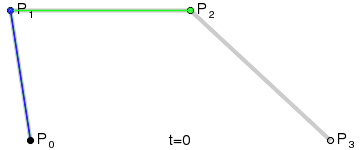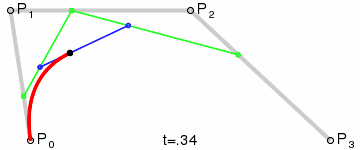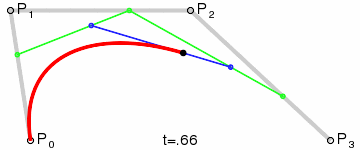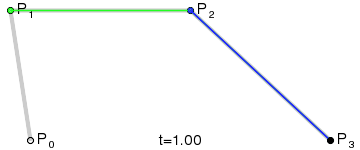
Step-by-step, we can determine the coordinates of all moving dots. First, we determine the location of the green dot that is moving between p0 and p1:

@keyframes green0 { from { --green0x: var(--p0x); --green0y: var(--p0y); } to { --green0x: var(--p1x); --green0y: var(--p1y); }
}

Additional green dots can be constructed in a similar way.

Next, we can determine the location of a blue dot like this:

@keyframes blue0 { from { --blue0x: var(--green0x); --blue0y: var(--green0y); } to { --blue0x: var(--green1x); --blue0y: var(--green1y); }
}

Rinse and repeat, eventually we will get the desired curve.

Similar to Method 2, with this method we can easily build a 3D Bezier Curve. It is also intuitive to extend the method for higher-order Bezier curves.

The only downside is the usage of @property, which is not supported by all browsers.

Animation Timing

All the examples so far have the “linear” timing, what about easing or other timing functions?

Note: By “linear” we mean the variable t of the curve linearly changes from 0 to 1. In other words, t is the same as animation progress.

animation-timing-function is never used in Method 2 and Method 3. Like other CSS animations, we can use any supported timing function here, but we need to apply the same function for all animations (move1, move2, and move3) at the same time.

Here’s an example of animation-timing-function: cubic-bezier(1, 0.1, 0, 0.9):

And here’s how it looks like with animation-timing-function: steps(18, end):

On the other hand, Method 1 is trickier, because it already uses a cubic-bezier(u1, v1, u2, v2) timing function. In the examples above we have u1=1/3 and u2=2/3. In fact we can tweak the timing by changing both parameters. Again, all animations (e.g., move-x and move-y) must have the same values of u1 and u2.

Here’s how it looks like when u1=1 and u2=0:

With Method 2, we can achieve exactly the same effect by setting animation-timing-function to cubic-bezier(1, 0.333, 0, 0.667):

In fact, it works in a more general way:

Suppose that we are given a cubic Bezier curve, and we created two animations for the curve with Method 1 and Method 2 respectively. For any valid values of u1 and u2, the following two setups have the same animation timing:

• Method 1 with animation-timing-function: cubic-bezier(u1, *, u2, *).
• Method 2 with animation-timing-function: cubic-bezier(u1, 1/3, u2, 2/3).

Now we see why Method 1 is “limited”: with Method 1 we can only cubic-bezier() with two parameters, but with Method 2 and Method 3 we can use any CSS animation-timing-function.

Conclusions

In this article, we discussed 3 different methods of moving elements precisely along a Bezier curve, using only CSS animations.

While all 3 methods are more or less practical, they have their own pros and cons:

• Method 1 might be more intuitive for those familiar with the timing function hack. But it is less flexible with animation timing.
• Method 2 has very simple CSS rules. Any CSS timing function can be applied directly. However, it could be hard to remember the formulas.
• Method 3 make more sense for those familiar with the math construction of Bezier curves. Animation timing is also flexible. On the other hand, not all modern browsers are supported, due the usage of @property.

That’s all! I hope you find this article interesting. Please let me know your thoughts!